by Johanna Serr
In parametric modelling, a geometry is generated using a function of the model f and numerical input parameters. In some cases, however, inverting the equation – hence extracting descriptive parameters from a geometry by finding f-1 – can be useful. The case presented below is motivated by hull shape optimization. However, the concept can be transferred to many other scenarios.
Aim
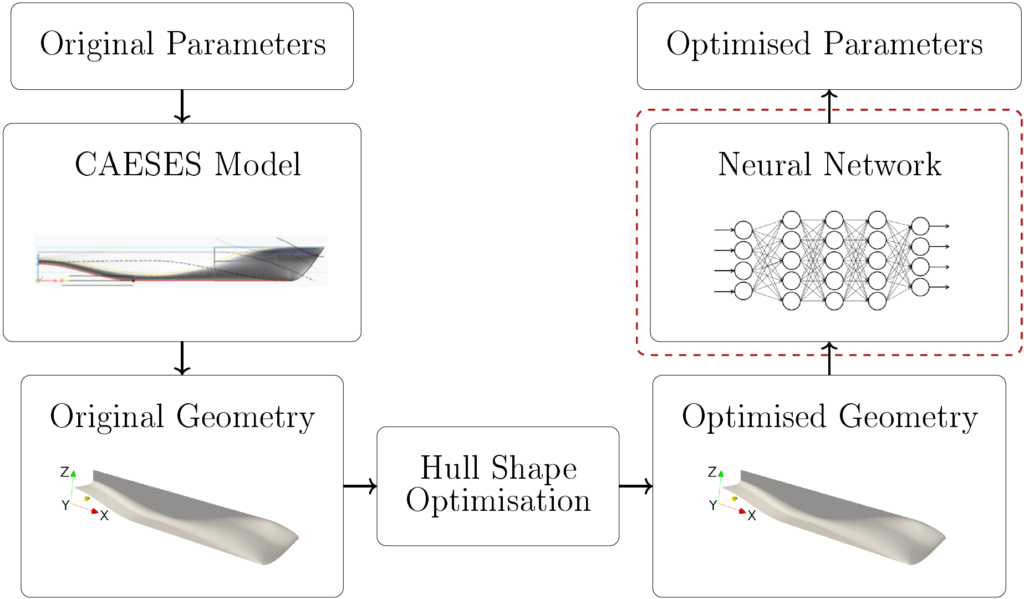
In the process of hull – or any kind of geometry-based – optimization, the problem of having to model a resulting geometry without knowing the exact values of characteristic parameters can arise. This can happen, e.g., in the context of a CAD-free optimization with an adjoint CFD solver, where a discrete representation of the geometry is deformed based on the adjoint sensitivities on the model surface. In order to open and further edit the optimized hull inside the CAESES environment, the parameter set belonging to the new geometry needs to be determined.
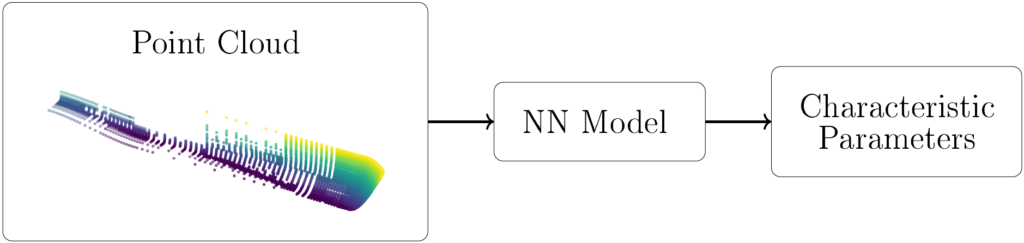
The use of neural networks offers a great opportunity to solve this kind of problem since they are a powerful tool for constructing a predictive model based on data. To process the data, the hull geometries can be represented by point clouds. The aim of this work is to develop a predictive model using neural networks (NN) that takes a point cloud as input and extracts characteristic parameters of the geometry.
Background Information
The concept behind neural networks originates in the field of bionics and is inspired by the human brain and the way biological neurons communicate with each other. The structure of neural networks allows the algorithm to learn patterns between given input and output data and to use the gained knowledge to make predictions about new, unknown data. Having this ability, neural networks work as a powerful tool in problems that contain a lot of data, while being too complex to be solved using traditional programming.
The structure of a simple neural network can be broken down to a single neuron, which mimics the way a biological neuron transports signals. From the numerical perspective, a neuron represents a set of inputs, weights and an activation function. The corresponding variables are initialized and tuned during the training process in order to map the input to output data. Stacking multiple neurons in parallel is called a layer. A more complex neural network consists of different types of layers like dense or pooling layers; each type having its own task and purpose. A special type of neural network is the convolutional neural network (CNN), which uses so called convolutional layers. This type of layer is suited for extracting pivotal features from input data and is mostly used in image-driven problems like image classification.
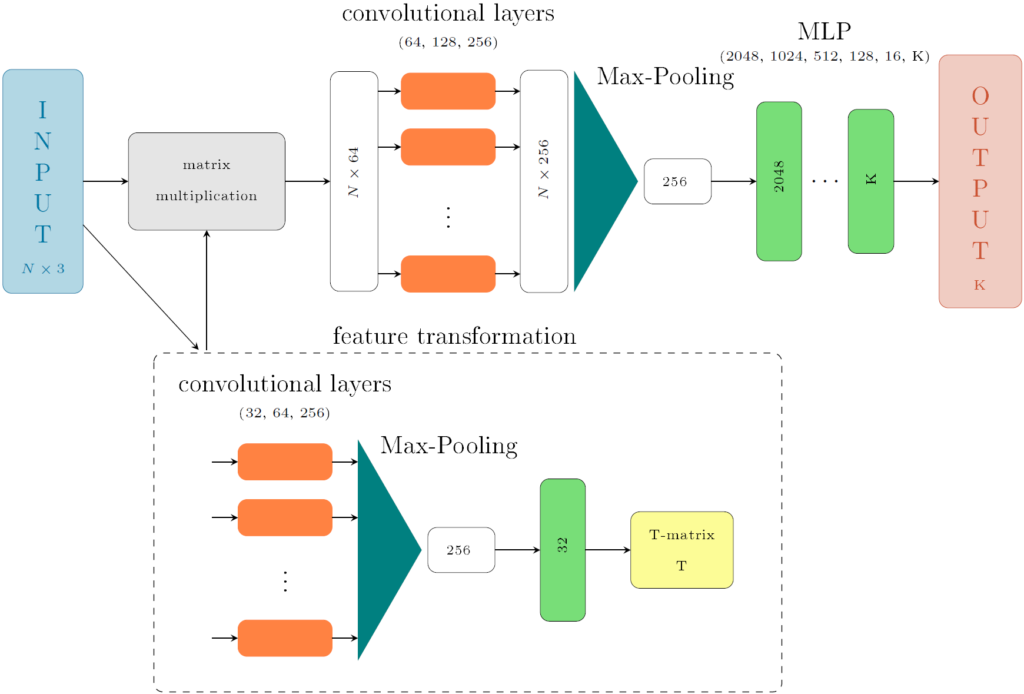
The CNN architecture developed in this work is inspired by pointNet, a neural network for 3D classification and segmentation based on point sets. For handling point clouds as input data, the irregular structure of the point cloud has to be considered.
The developed neural network takes a point cloud of size Nx3 as input; N being the number of points inside of the 3D point cloud. Inside a mini-network, a feature transformation is executed in order to make the data invariant to permutations. Following the matrix multiplication, the features are being further extracted using convolutional and Max-Pooling layers. In a final step, a regression is carried out using multi-layer perceptrons (MLP) and the output consisting of K descriptive parameters is generated.
The main goal of developing a neural network is creating a predictive model that has the capability of generalization – the ability to make accurate predictions not only on training data but also on new, unseen data. For testing this property, the data set can be split into a training and a test set. The model is trained using the data from the training set; after training the model is tested using the unseen data from the test set. Comparing the performances of the model on the training and test set, a statement about the capability of generalization can be made.
Creating the Dataset using CAESES
The data set is created using a hull model provided as sample in CAESES. Using the parametric modelling functionality, four parameters are set as design variables, which allows access to these parameters in batch-mode. Two different types of parameters are chosen – lengths and angles. Each parameter is varied within a given interval, thereby creating a data set of 4000 hull geometries with unique shapes. The main dimensions, i.e., length overall, height, and width are fixed to ensure a constant bounding box of all geometries.
The influence of the selected parameters on the hull shape is illustrated as follows.
LENGTH OF FLAT SIDE

STEM LENGTH

WATERLINE ENTRANCE ANGLE
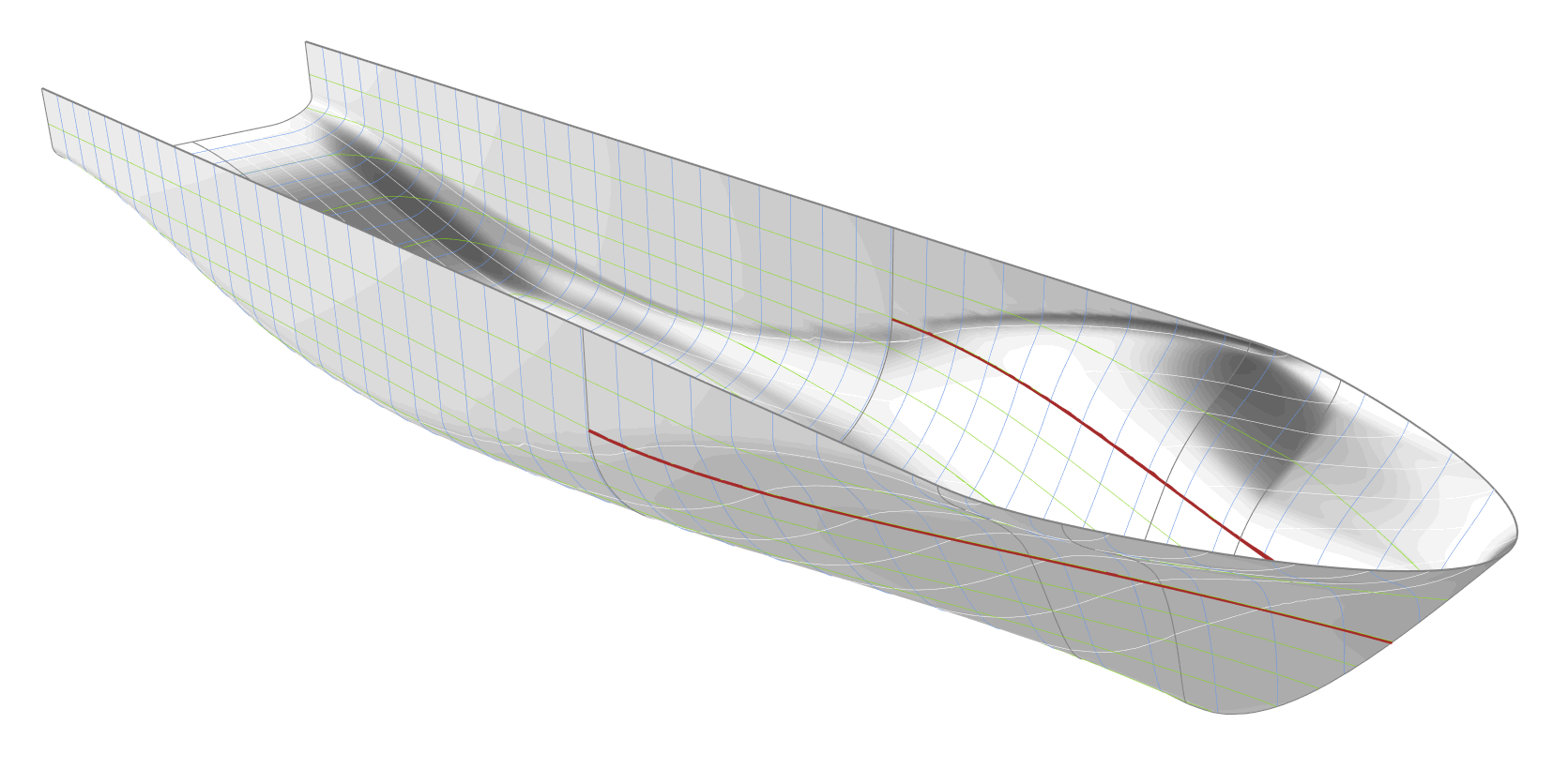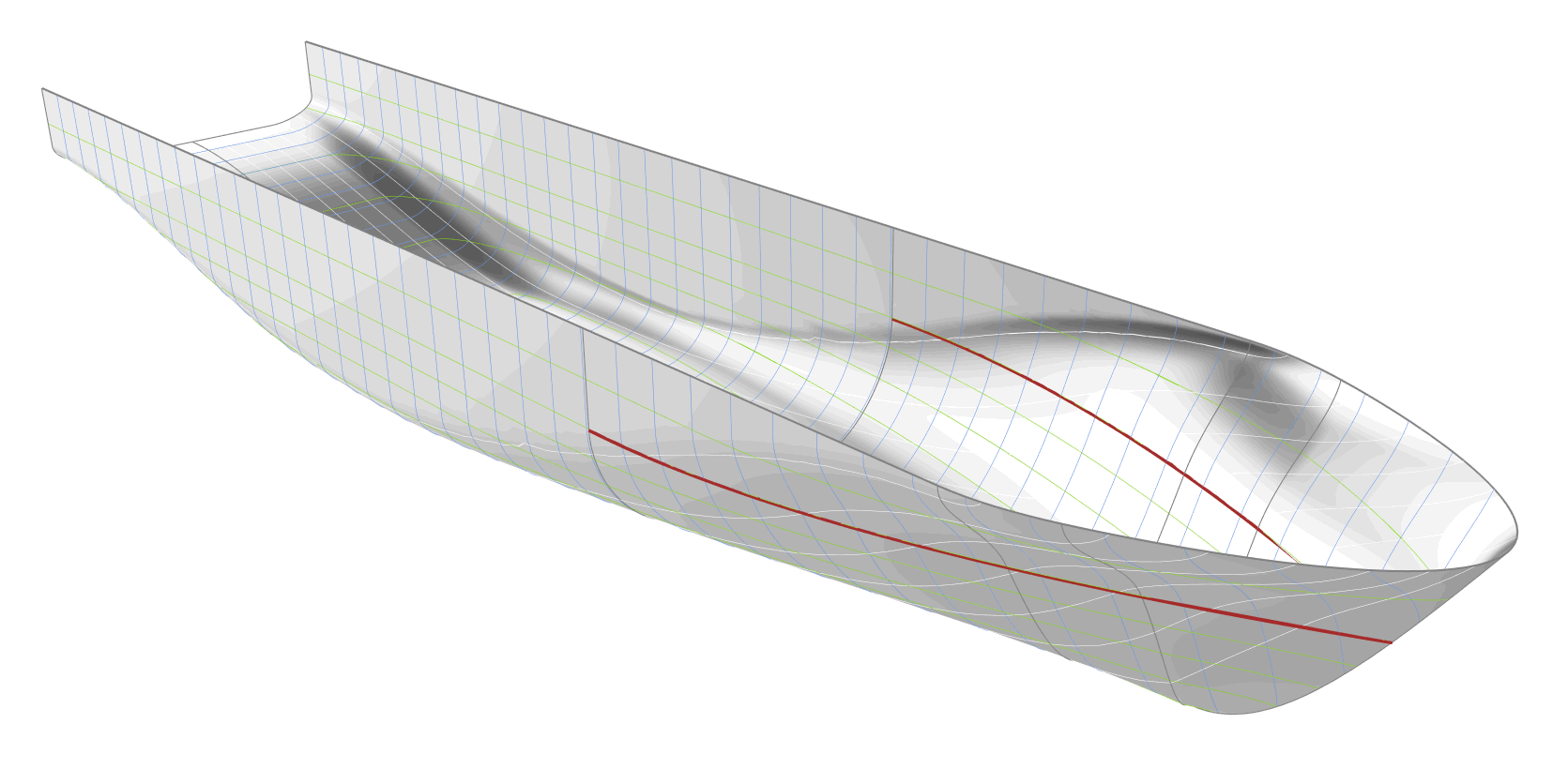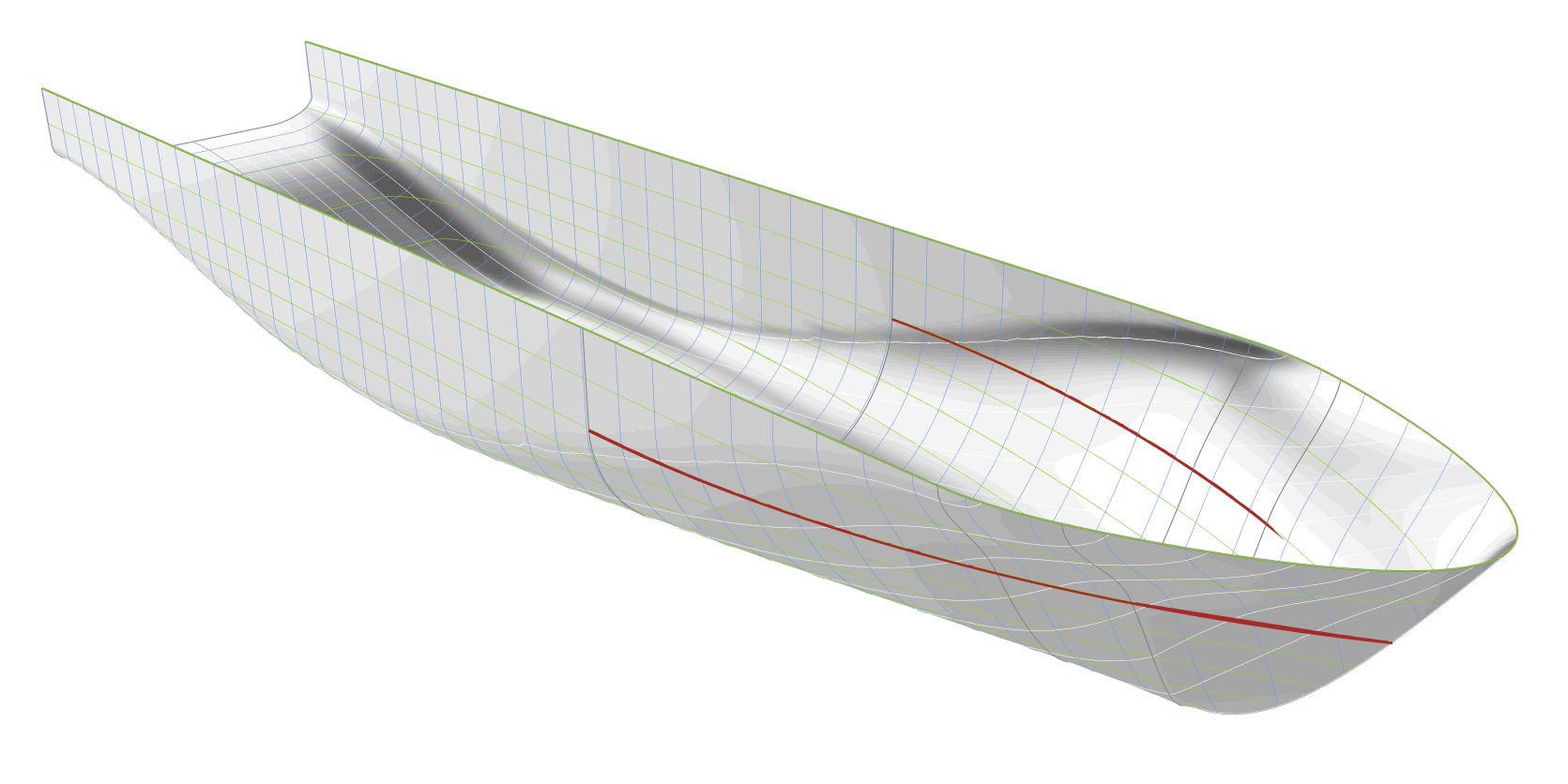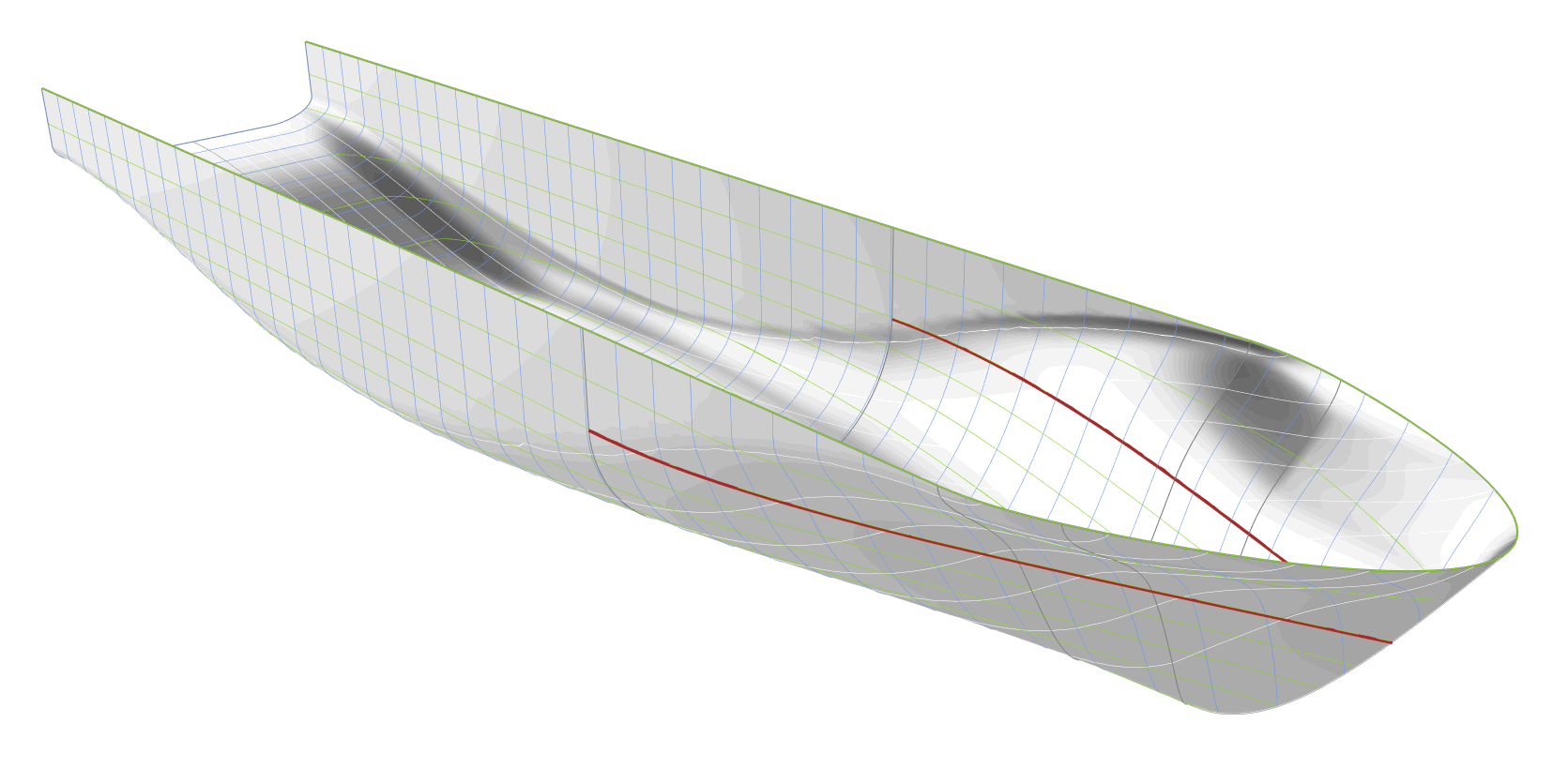
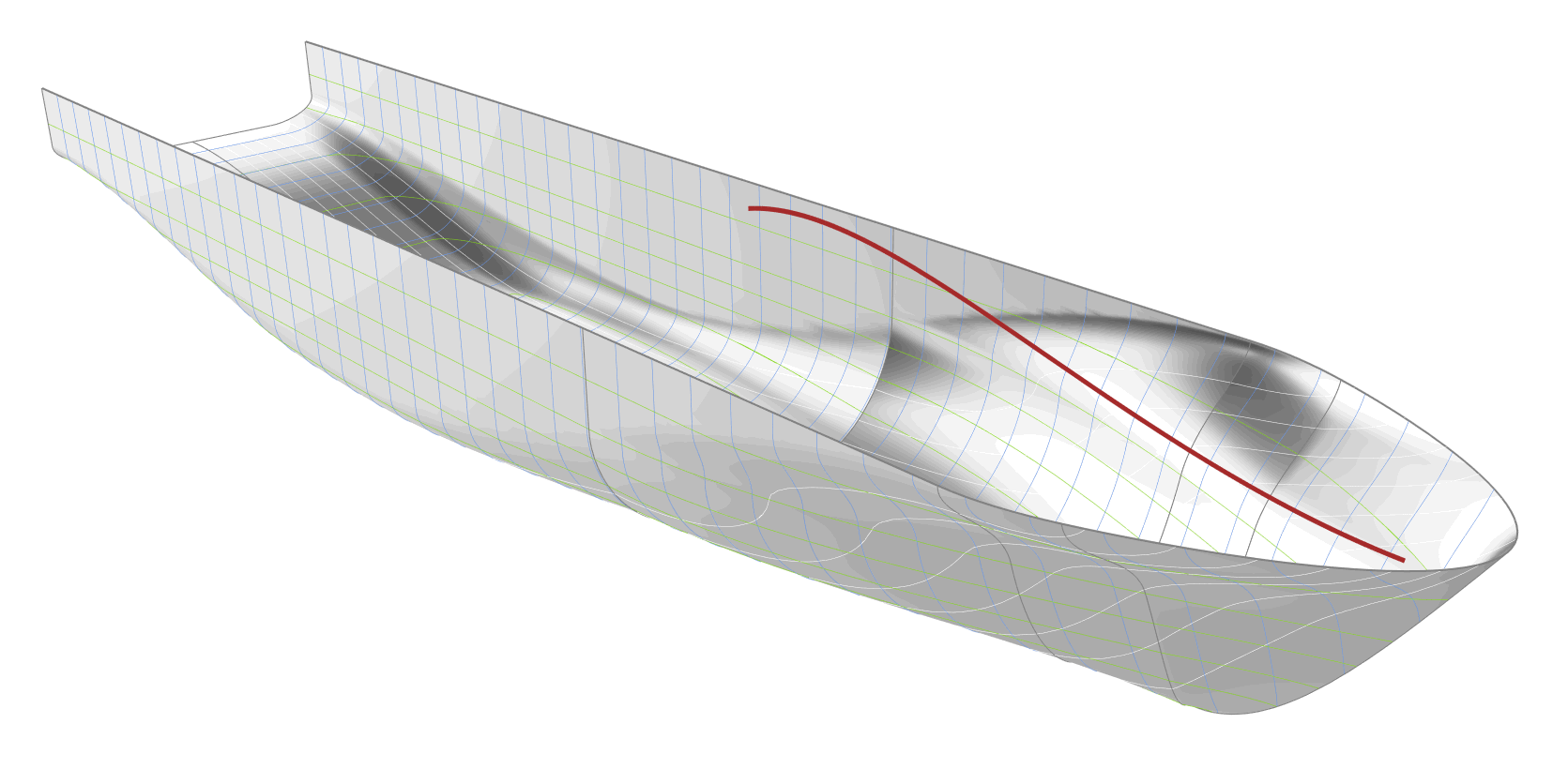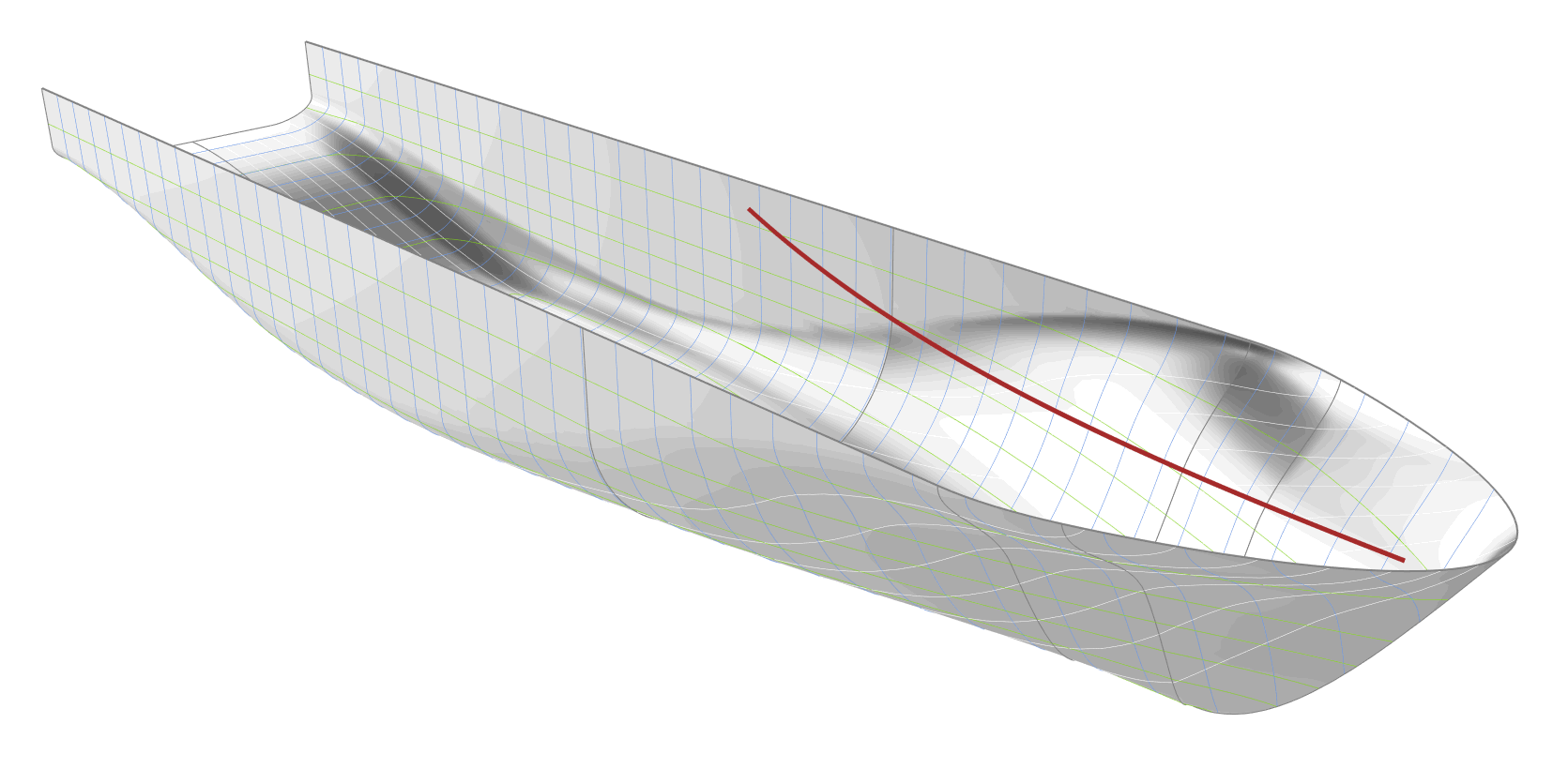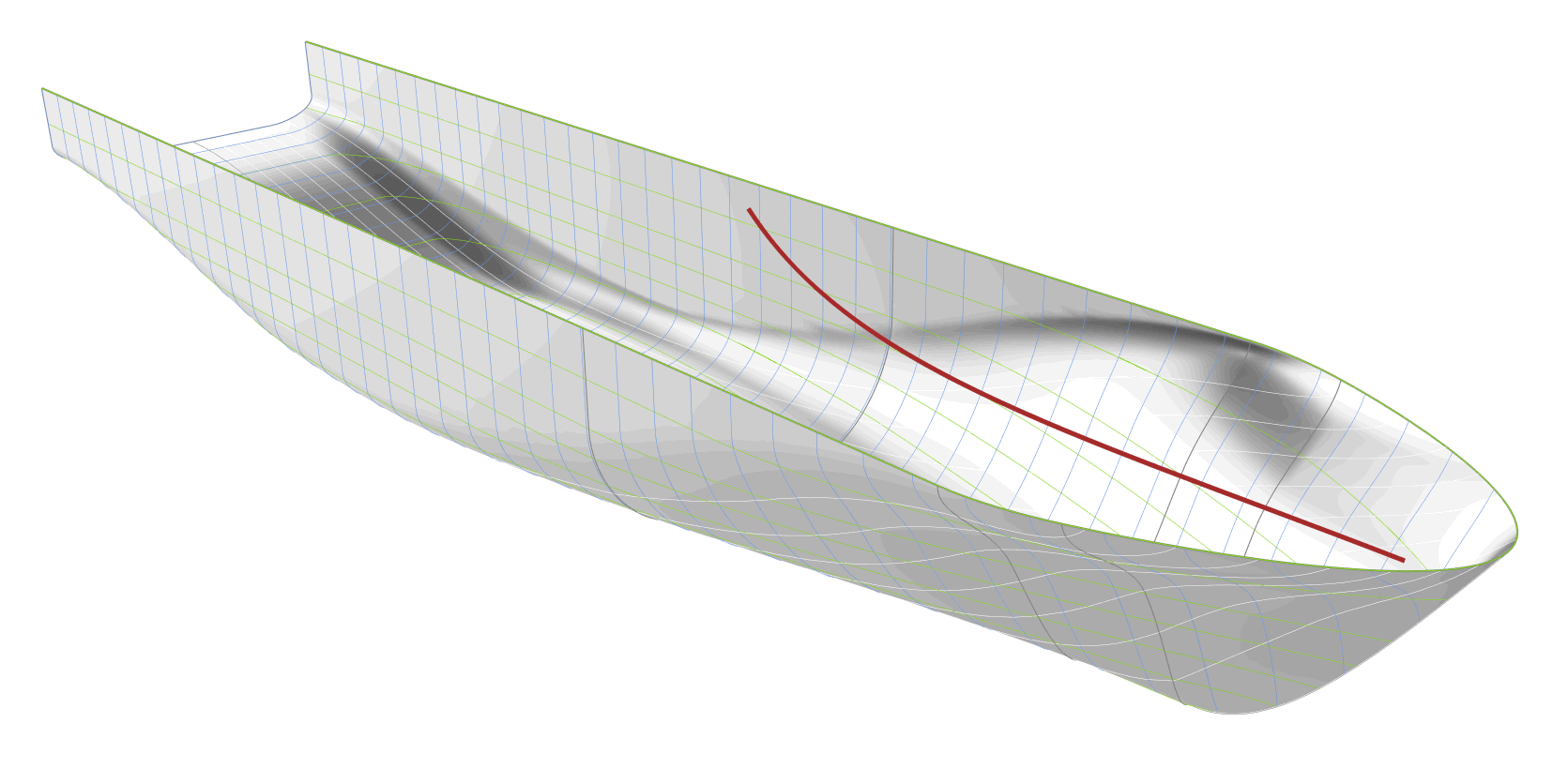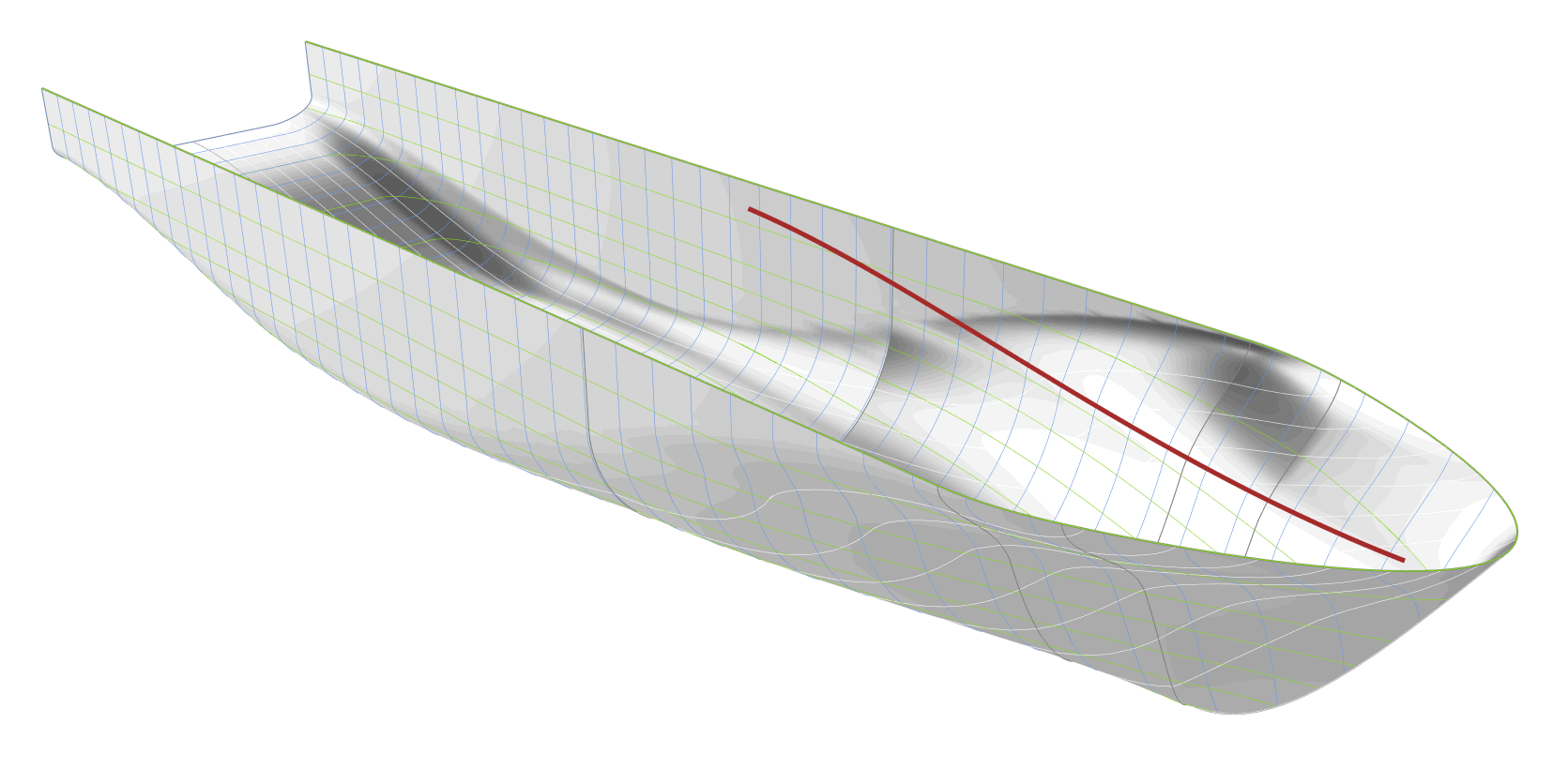
FRAME GRADIENT AT THE WATERLINE DISTRIBUTION
The curve defining the gradient of the frames along the waterline, shown as red curve in the following animation, is controlled by the tangent angle at the start. A low value for the tangent angle causes a high section gradient at the waterline close to the forward shoulder, and thereby, a bulkier hull. Although out of all the parameters this one is varied within the largest interval, its variation has the least impact on the shape of the hull.

After automatically generating the geometries in batch-mode in CAESES, the point clouds are extracted using a random uniform distribution on the surface of the hull.
Results
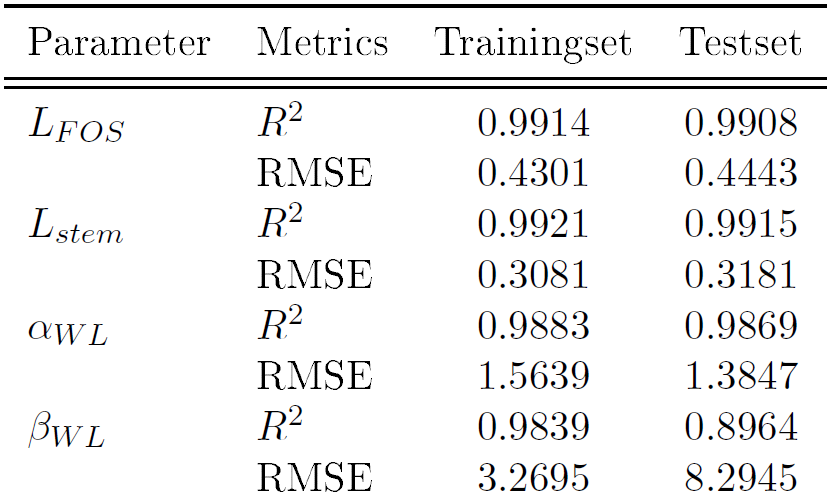
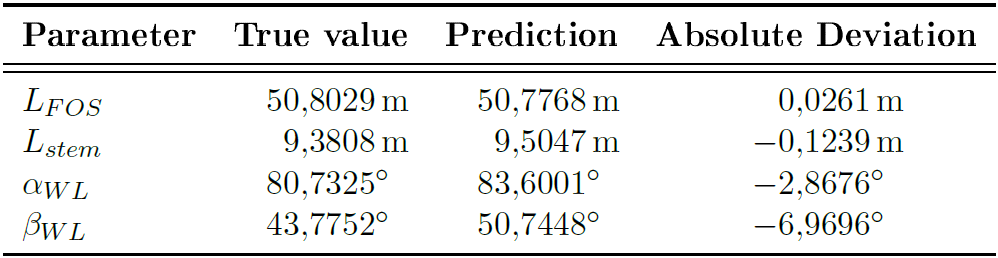
The training of the neural network is executed using the Keras and Tensorflow libraries. As validation method, the k-fold cross validation is carried out using k = 5; resulting in a training set size of 3200 and test set size of 800. The size of the point cloud is set to N = 1024 points. The results of one representative training cycle are listed in the table below.
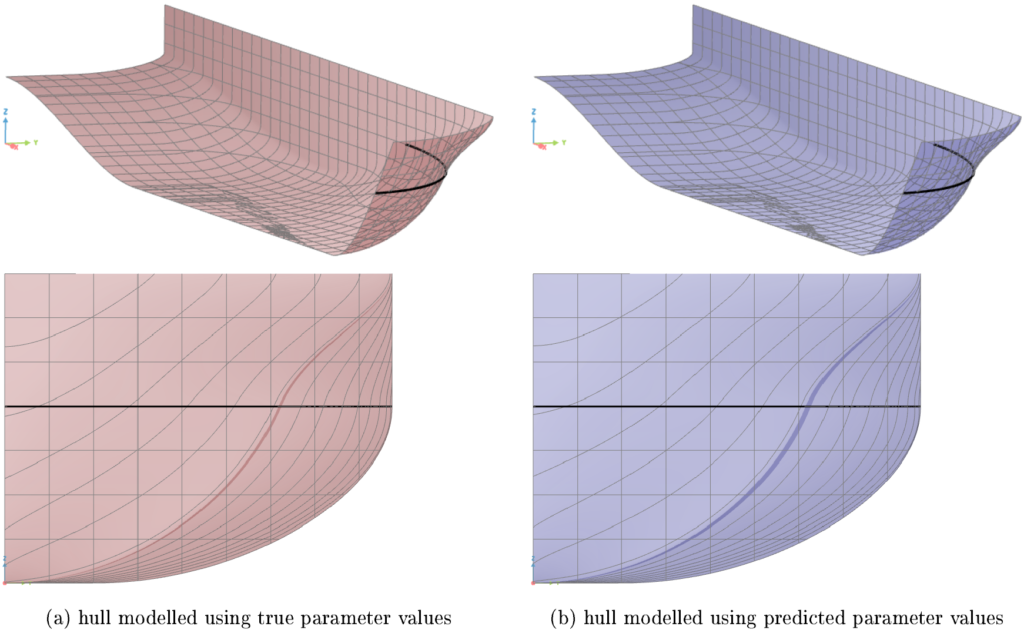
The neural network model is able to achieve high values for the R2 score in training and test set. However, compared to the other parameters, the parameter βWL scores the lowest. This can be explained by the fact that the variation of the angle βWL has the smallest impact on the general hull shape, in comparison to the three other parameters, hence making the prediction of βWL a more complex problem. Using a more complex neural network could result in a more accurate prediction of βWL. To make the results more tangible, a single example is chosen from the test set and the hull is modelled using true and predicted values.
Visually comparing both hulls, their geometries show a great resemblance. As expected, the prediction of the angle βWL shows the greatest absolute deviation from the true value. However, as it has the least impact on the general hull shape, its deviation of almost 7° is hardly noticeable in the resulting geometry.
Conclusion
In this study, a method of mapping geometry to parameter data is investigated in order to create a predictive model which is able to find descriptive parameters for a given geometry. Neural networks are used in the development of this method. The results show that the established neural network is able to make accurate predictions.
Two different types of parameters – lengths and angles – are tested and no difference in performance is found. However, looking at the parameter βWL, the impact of the parameter on the geometry shape has an influence on the performance and accuracy. It is concluded that the smaller the impact of the parameter, the more complex the problem and the less accurate the prediction.
About the Author
Johanna Serr is a graduate student of mechanical engineering at the Technical University Hamburg-Harburg (TUHH) with a specialization in numerics and informatics. Her special field of interest is computational fluid dynamics. The study presented here is part of her project thesis.
“With the help of CAESES I was able to create the dataset for my research with minimal effort. The parametric modelling functionality in CAESES as well as the easy access to the variables in batch-mode were especially helpful. These two features combined, CAESES turned out to be a powerful instrument and a key component for the progress of my study.
Working with CAESES is very intuitive. Thanks to the well-written and detailed tutorials, I was quickly able to learn how to navigate inside of the CAESES environment and integrate the CAESES functionalities into my automated workflow.”
– Johanna Serr, MSc Student at the TUHH