In the maritime industry, there is a growing demand for energy efficiency and emission reductions to meet environmental regulations. Traditional propeller designs are no longer sufficient, prompting the need for unconventional designs, such as tip-rake propellers, that can improve fuel efficiency and minimize environmental impact. Computational Fluid Dynamics (CFD) has revolutionized propeller design by allowing for in-depth exploration of the design space and optimization of propeller geometry for enhanced efficiency and performance. Furthermore, surrogate modeling has evolved significantly in recent years, offering accelerated solutions for complex design tasks by leveraging simulation results to provide instant insights into propeller performance. This streamlined approach not only improves efficiency, but also facilitates the exploration of a broader range of design alternatives, resulting in innovative and optimized propeller solutions.
Literature Data
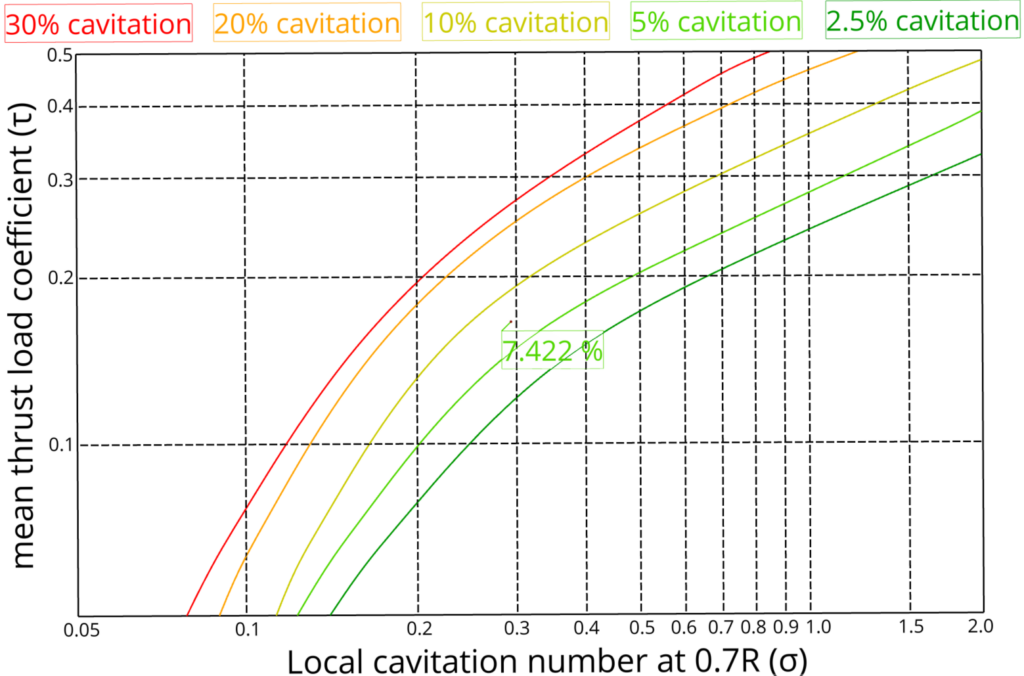
The literature data incorporated in this study focuses on Wageningen B-series propellers, renowned for their extensive usage in marine propulsion. One notable advantage of the B-series is the ability to swiftly calculate open water characteristics due to the implementation of polynomial regression based on experimental results [1]. Additionally, the Burrill Diagram, a widely recognized criterion for fixed-pitch conventional propellers in the preliminary design stage [2], had been digitized within CAESES® for this study.
Parametric Model for Unconventional Propellers
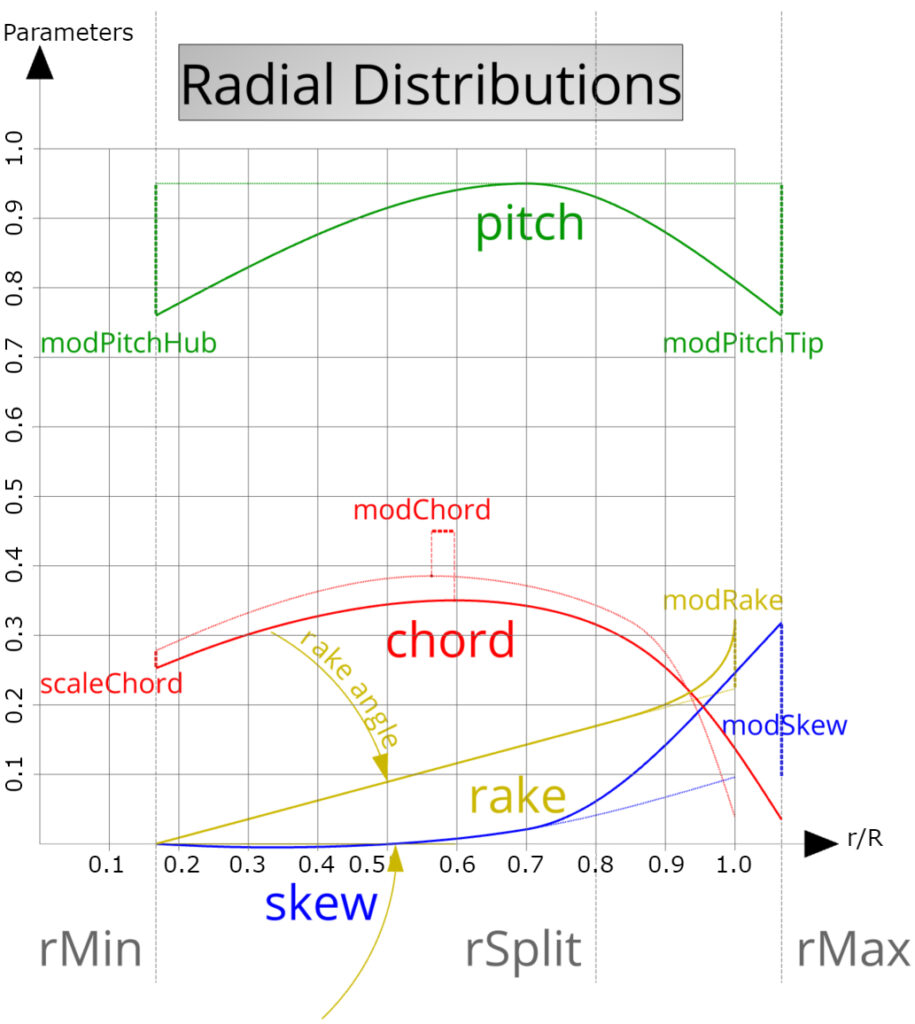
The Parametric Model for Unconventional Propellers (PMUP) was set up and parametrized in CAESES®. It allows for the modification of existing propeller designs to add features like tip rake and high skew angles. By adjusting key radial distribution functions such as pitch, chord, skew, and rake using specific design variables, the PMUP transforms conventional propeller designs into unconventional ones. Especially parameters like modRake and modSkew are essential for the generation of unconventional propellers, allowing detailed control over the tip region.
| Design Variables | Range | Description |
|---|---|---|
| modPitchHub | [-0.2,0] | Modifies pitch at hub |
| modPitchTip | [-0.2,0] | Modifies pitch at tip |
| modChord | [-0.1,0.1] | Moves the position of max. chord |
| scaleChord | [0.9,1.1] | Scales the overall chord size |
| modRake | [-0.15,0.15] | Modifies rake at tip |
| rakeAngle | [-20,20] | Defines the rake angle |
| modSkew | [0,0.15] | Modifies skew at tip |
| splitRadius | [0.7,0.9] | Defines where modRake is enabled |
Numerical Simulation Setup
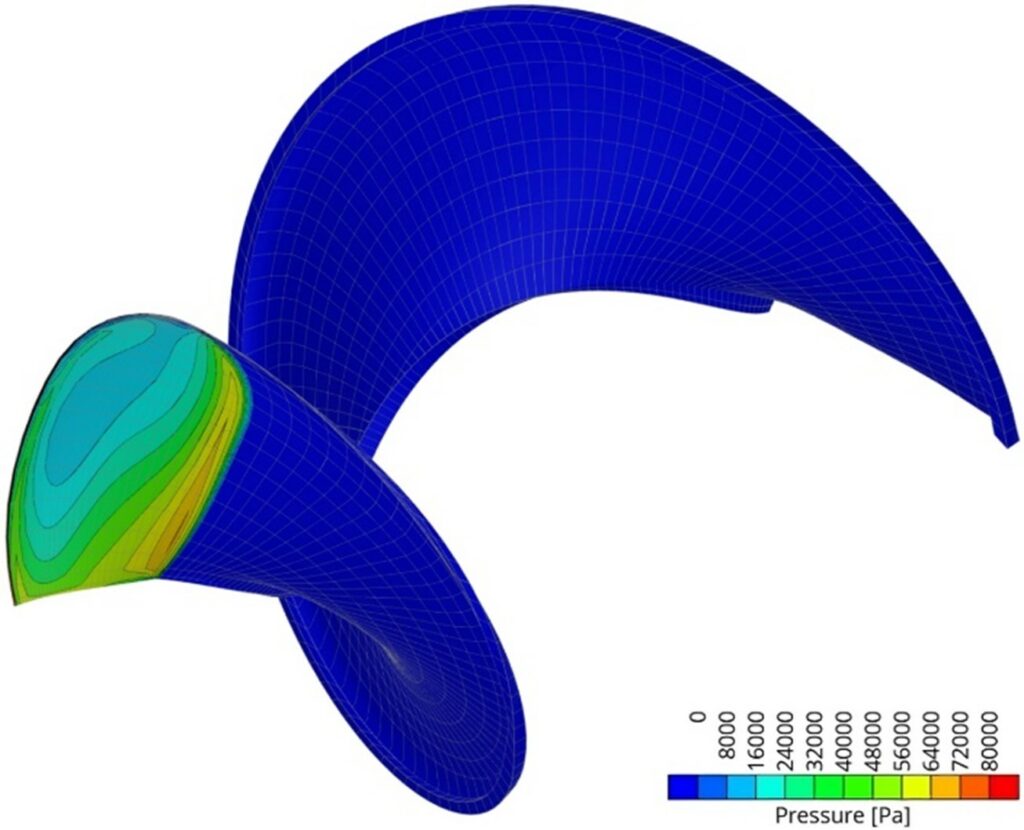
The blade geometry modeled in CAESES®, represented as a NURBS surface, was transformed into a panel mesh as input for the simulations. The mesh configuration included 30 chord-wise and 20 span-wise panels, determined through sensitivity analysis. Denser spacing was allocated at the leading edge and tip of the blade. A sharp trailing edge was implemented to satisfy the Kutta condition for accurate simulations. The hub geometry was not included in the modeling process, as illustrated in the Figure below.
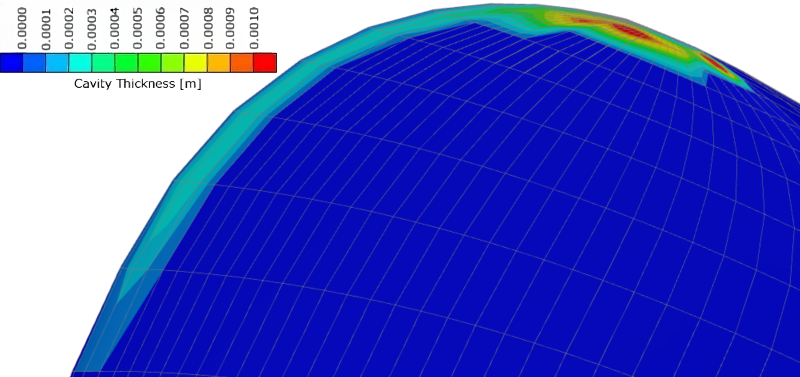
A Blade Element Momentum (BEM) code (panMARE from TUHH; based on potential theory) was used to analyze the fluid flow around the propeller blades [3]. Open water tests were conducted to evaluate the propeller performance. A heuristic model accounted for flow friction effects. Cavity area and volume were calculated to assess cavitation, providing insights for the propeller design optimization.
Optimization Framework
Optimization Algorithms
Firstly, a Design of Experiments (DoE) applying the Sobol method uses a quasi-random sequence to homogeneously distribute designs and scan the design space.
Secondly, the tangent search method (T-Search) focuses on single-objective optimization, employing tangent moves within hyperspace, although it requires a carefully chosen initial point and may converge to local minima. Usually, the best Sobol design is a promising candidate as a starting point for the T-Search optimization.
Lastly, Response Surface Methodology (RSM) constructs input-output surrogates using the Kriging method, enabling finding optimal solutions without simulations, with a sample size requirement of at least five times the input vector size (design variables used in the optimization process).
Input Parameters
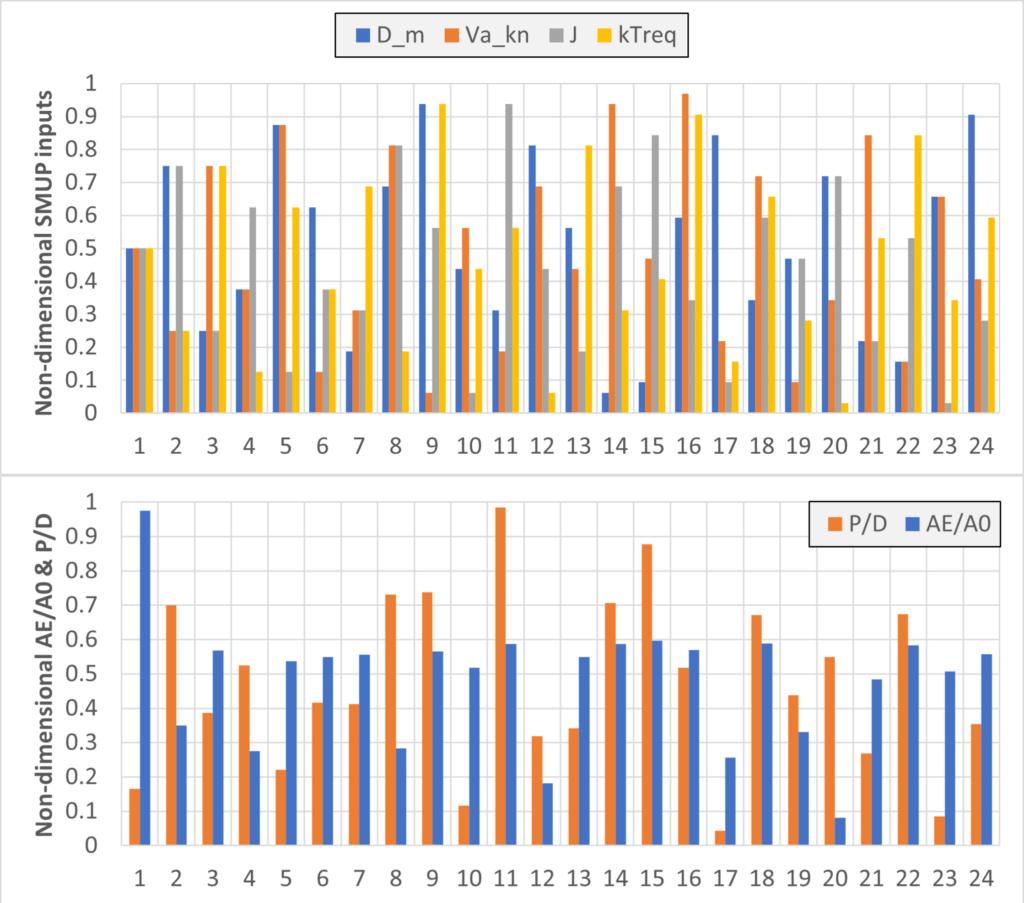
The main goal was to develop efficient propeller designs suitable for commercial vessels. Key parameters such as propeller diameter and inflow velocity, chosen within a range tailored for commercial applicability, significantly impact performance characteristics. Utilizing non-dimensional coefficients enhances design flexibility across diverse operational conditions. Integration of 5-bladed propellers meets modern design standards. The Sobol method efficiently explores the design space, analyzing input parameter sensitivity and the influence on propeller performance.
| Inputs | Range | Units | Description |
|---|---|---|---|
| D | [6,8] | meters | Diameter of the Propreller |
| VA | [18,22] | knots | Inflow Velocity |
| J | [0.45,1.25] | Advance Coefficient | |
| kTreq | [0.05,0.2] | Required Thrust Coefficient | |
| Z | 5 | Number of Blades |
Optimization Process
The optimization was performed in CAESES and adopted a dual-phase approach aimed at maximizing propeller efficiency, minimizing cavitation and meeting required thrust. T-Search optimization was employed in both phases. In the initial phase, the optimization relies on the aforementioned input parameters, tailored to a B-series setup. Utilizing B-series polynomials to assess the open water characteristics and the Burrill diagram to estimate the cavitation, eliminates the need for simulations. In the subsequent phase, panMARE simulations were conducted using the parametric CAESES model to optimize both conventional and unconventional designs. This approach ensures manageable design space dimensionality, shape diversity, and suitable constraints. The initial values in this phase were derived from the optimal B-series designs identified in the first phase.
| 1st Phase | 2nd Phase | |
|---|---|---|
| Name | B-series setup | Unconventional Propeller setup |
| Algorithm | T-search | T-search |
| Initial Values | 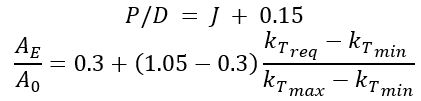 | Optimal B-series design from the 1st phase |
| Open Water Tests | B-series polynomials | panMARE |
| Cavitation | Burrill Diagram | panMARE |
| Find | P/D , AE / A0 | Design variables of Parametric Model for Unconventional Propeller |
| Objective Function | maximize propeller efficiency η0 | maximize propeller efficiency η0 |
| Constraints | c=Burrill(σ0.7R,τc ) < 30% Treq ≤ Tpan ≤ 1.3Treq | Acav < 0.1 AE Treq ≤ Tpan ≤ 1.3Treq |
Optimization with CAESES and panMARE
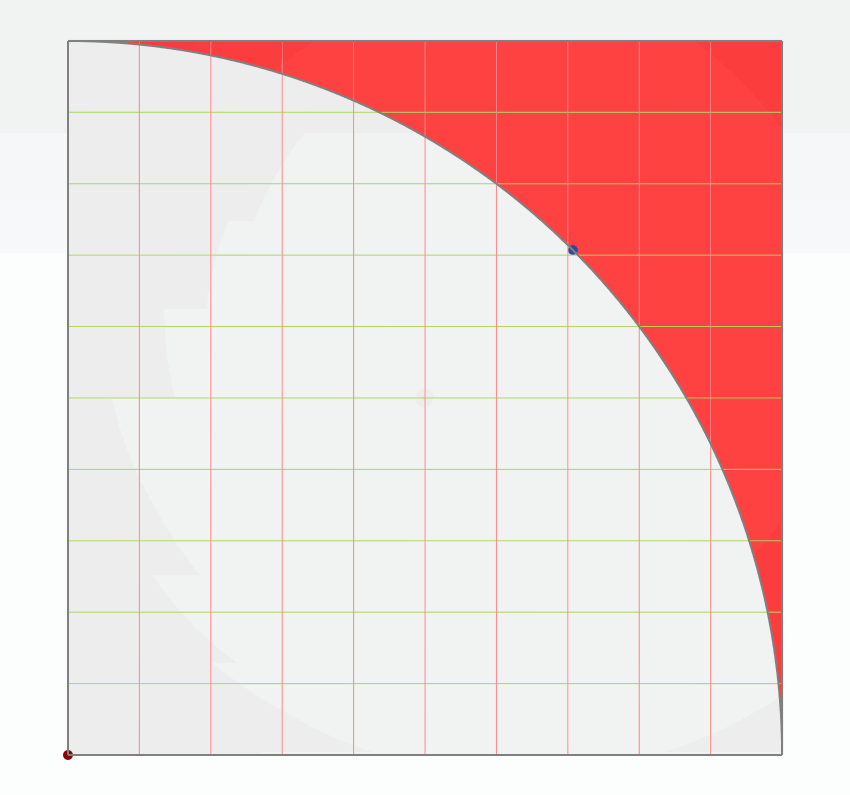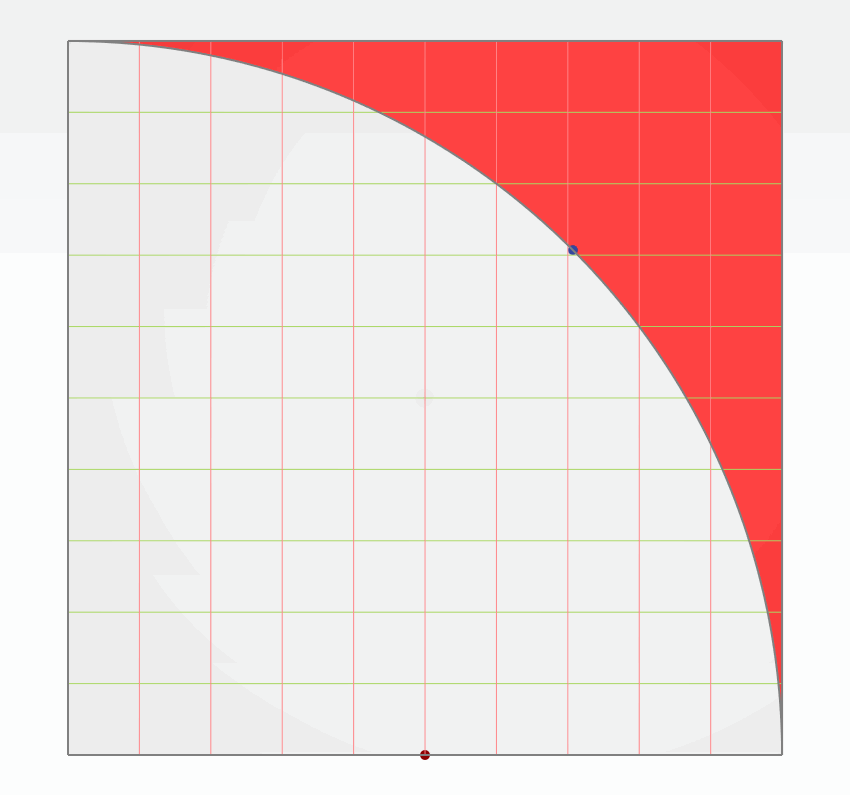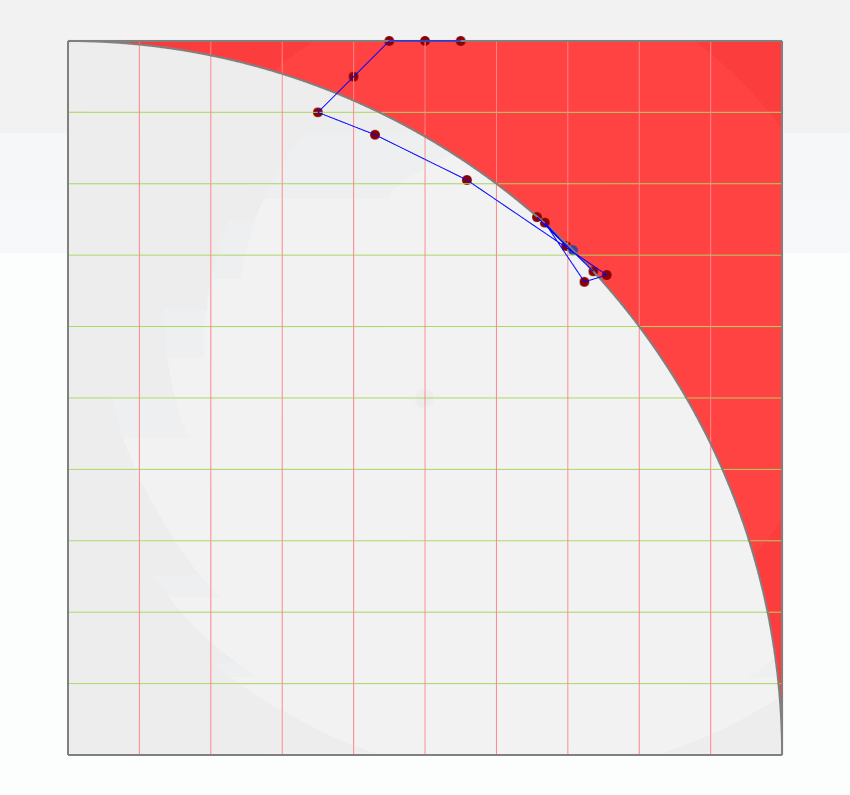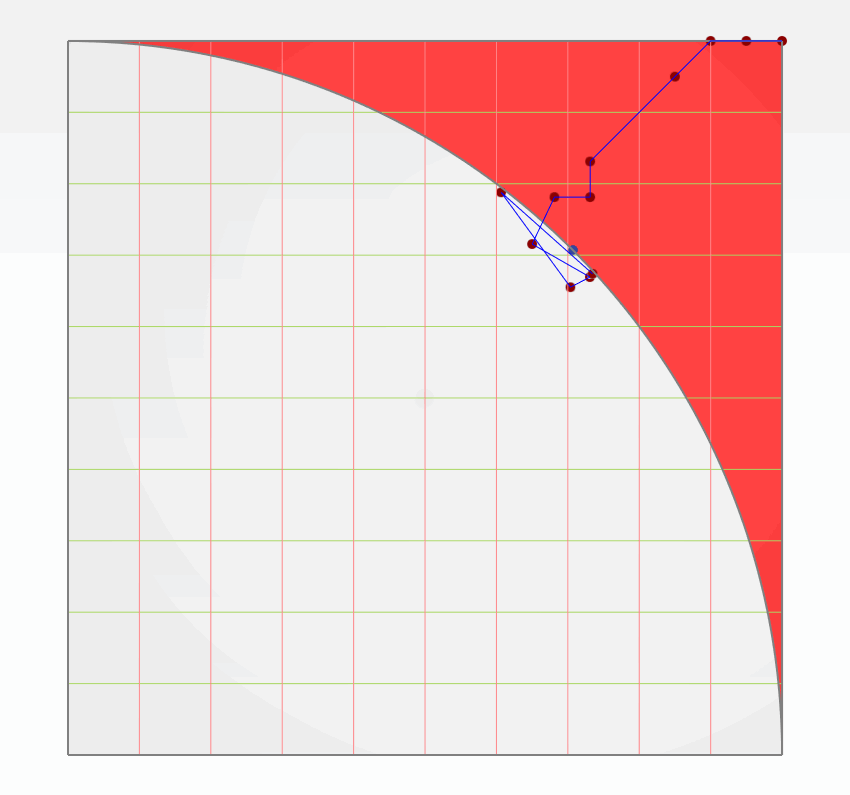
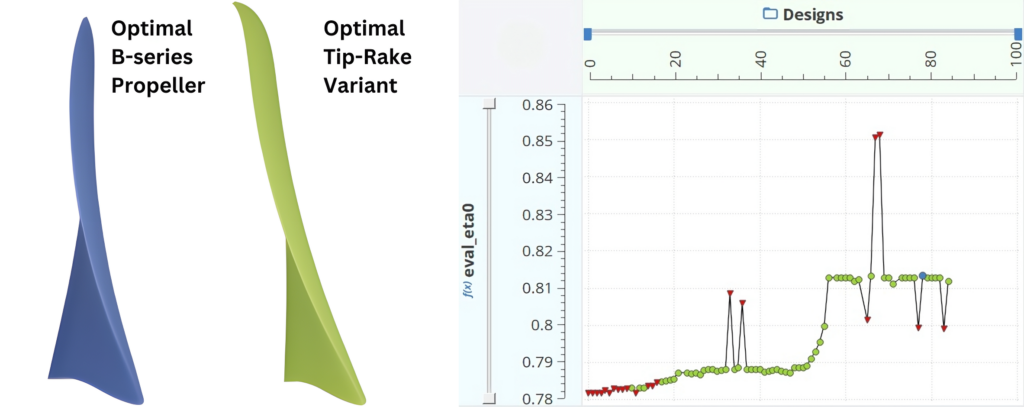
As an exemplary configuration, to demonstrate this optimization phase, a diameter of 7 m, an inflow velocity of 20 knots, an advance coefficient of 0.85, a required thrust coefficient of 0.125, and 5 blades were used. The convergence history of the second optimization is depicted in the figure below. The initial T-Search evaluation yields a B5-73 propeller, representing an optimal B-series propeller. Subsequently, the optimization aims at finding a tip rake propeller with targeted thrust, limited cavitation, and enhanced efficiency. Red triangles indicate design instances violating constraints, while green circles denote feasible designs. The blue circle highlights the optimal tip rake variant with the highest efficiency. Instances with overestimated efficiency have higher thrust than desired, whereas those with underestimated efficiency exhibit lower thrust values.
Building the Surrogate Model
The workflow of building the Surrogate Model for Unconventional Propellers (SMUP) employs the aforementioned dual-stage optimization process originating from a vector of four primary inputs and resulting in an unconventional propeller design. This yields two results: a vector detailing the geometry’s design variables values and another capturing the open water characteristics, augmented with cavitation estimates. Subsequently, this optimized data set is fed into the surrogate model for training purposes, with the final target of being able to use the surrogate model to quickly and accurately predict the optimization outcomes and the optimal propeller geometry from just the four primary inputs, bypassing the extensive simulation phase.
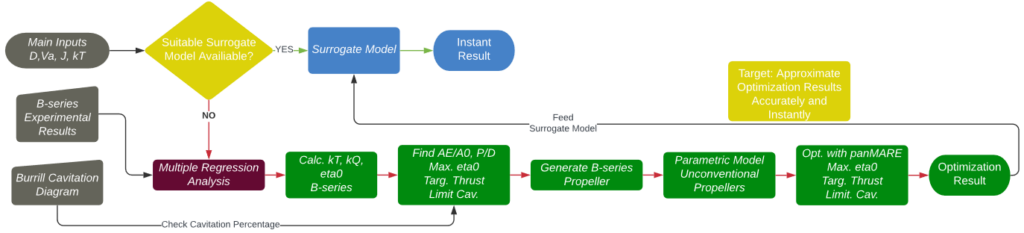
Optimization Results
An Sobol sequence efficiently generated a set of 24 input vectors, which serve as the initial training data set for the surrogate model. The figure below (top left) shows how the design space was effectively explored. B-series based optimization identifies the most efficient propeller, focusing on thrust and cavitation limitations, with propeller geometry determined by expanded area ratio and pitch ratio (bottom left).
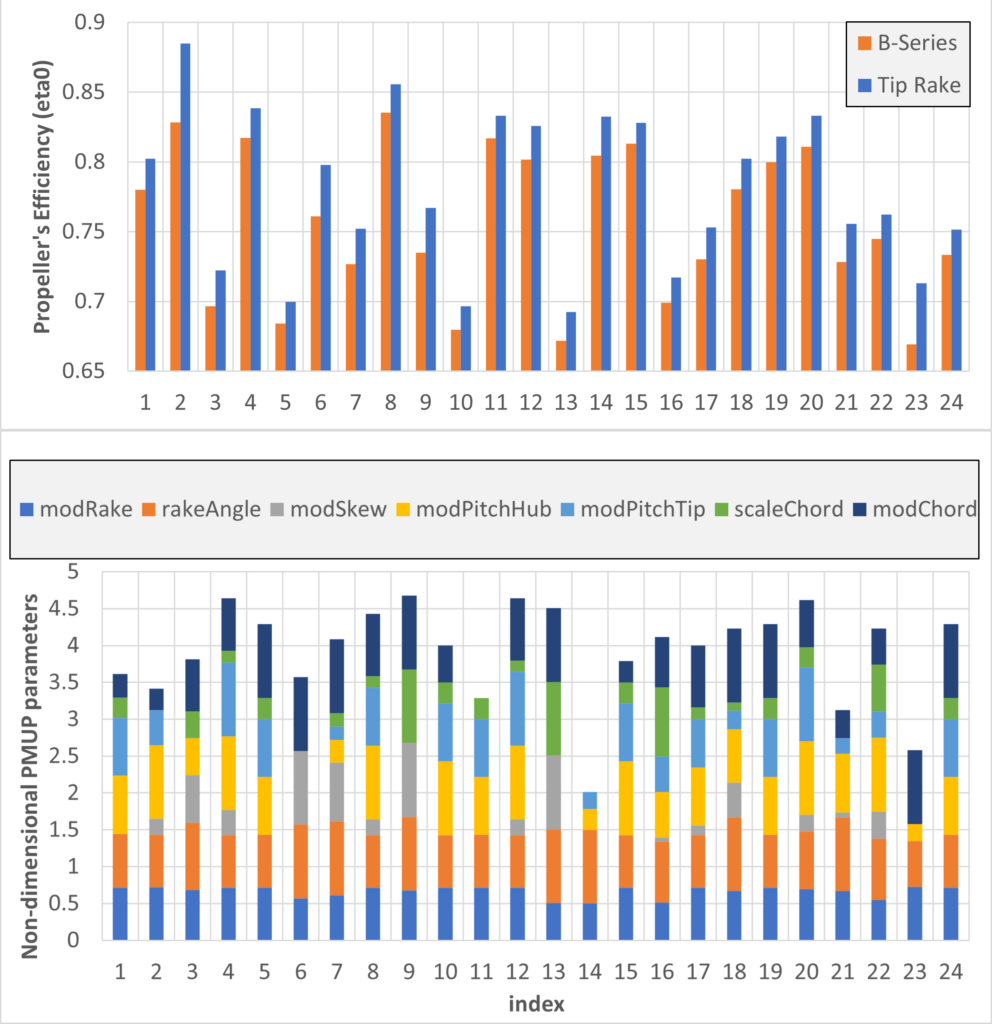
Following the simulation-based optimization phase, enhanced performance of tip rake designs is evident (top right), with an average increase of approximately 3.3% in efficiency. Design variables (bottom right) indicate a tendency towards backward and tip rake propellers, like Kappel propellers, with low chord values proving effective. However, modifying the skew curve seems less preferable, as B-series propellers already possess a favorable skew curve.
Conclusion and Outlook
A successful parameterization of tip rake propellers and a dual-stage optimization approach led to unconventional designs with enhanced efficiency. This streamlined workflow seamlessly integrates insights from literature and simulation data inside CAESES. The surrogate model generated on the basis of a training data set from previous optimization runs performs effectively, facilitating the identification of emerging patterns in the optimal outcomes of unconventional designs, particularly with back rake and tip rake propellers.
However, it should be mentioned that challenges in the surrogate model development occurred, notably in extrapolation. It is essential to minimize data noise to resolve discrepancies between predicted simulations and optimization outcomes. This requires refining the parametric model through an iterative trial-and-error process, which may take some time due to its complexity. Moving forward, further plans encompass incorporating not only B-series profiles, but also NACA66 profiles, integrating ship hull wake field data using panMARE, and accommodating 3-bladed and 4-bladed propellers. The ultimate objective is to establish a robust tool for early-stage marine propeller design.
Acknowledgment
This research was conducted as part of the research & development project DeffProForm, funded by the Federal Republic of Germany, Federal Ministry for Economic Affairs and Energy (now Federal Ministry for Economic Affairs and Climate Action) on the orders of the German Bundestag (Förderkennzeichen 03SX516C).
References
[1] Barnitsas, Michael M., D. Ray, and P. Kinley. KT, KQ and efficiency curves for the Wageningen B-series propellers. University of Michigan, 1981.
[2] Burrill, L. C., and A. Emerson. “Propeller cavitation: Further tests on 16in. propeller models in the King’s College cavitation tunnel.” International Shipbuilding Progress 10.104 (1963): 119-131.
[3] panMARE code. Availiable via: https://www.tuhh.de/panmare/home