The polycurve type in CAESES® is something that gets used quite a lot, in particular in the context of surface generation through the meta surface technology where you need to have a single curve definition. The polycurve simply takes a set of N curves and represents a single curve with an own curve domain based on this input. Curve domains typically run in the interval [0,1]. The interesting thing is that the curve domain is then defined according to the number of input curves.
See the following illustration:
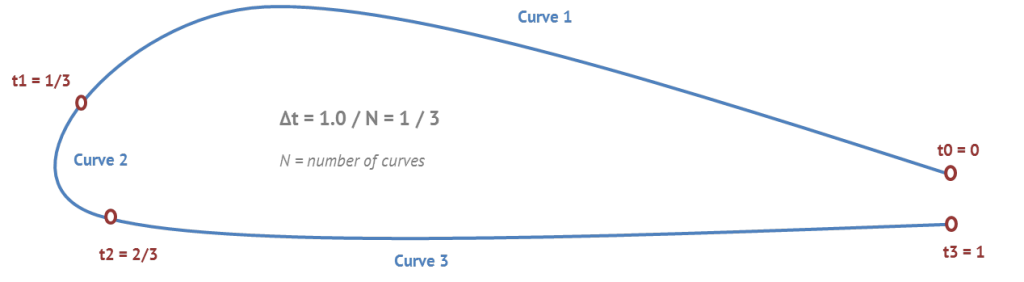Let’s assume you want to get the exact end position of the first input curve. For N=3 input curves of a polycurve, the polycurve parameter is simply t1=1/3. The connecting parameter locations are defined by t_i = i * 1 / N where N is the number of input curves, and i runs from 1 to N-1.
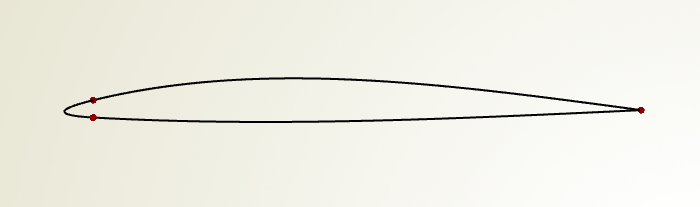
Here is an example where the screenshots are taken from CAESES®. A simple profile gets modeled which runs from the trailing edge (right-hand side) via the leading edge back to the trailing edge. Three curves are generated separately and then put into a polycurve:
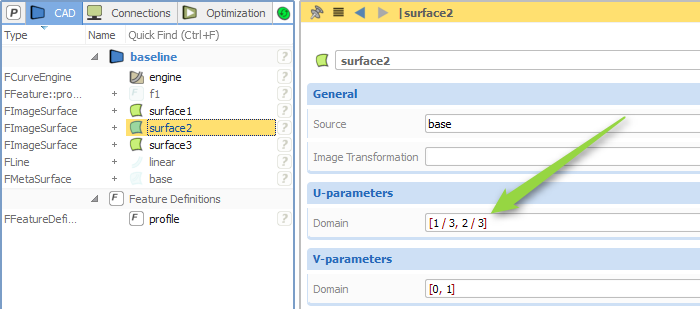
If you now create a 3D surface (say a lofted surface or a meta surface) from such a profile, you can directly split the generated surface in order to have the individual surface patches available. This is helpful when you need to split a single 3D surface into several pieces e.g. for more control in the meshing process and the simulation. See the following screenshot:
In this example, three image surfaces are created based on the single 3D surface. The next screenshot shows how the second surface i.e. the leading edge gets defined:
The surface u-direction (“U-parameters”) corresponds to the profile definition, while the v-direction is the sweep direction in this demo example. Just for interested readers and to complete this short blog post: Check out the feature definition of the profile from which the single surface gets created…
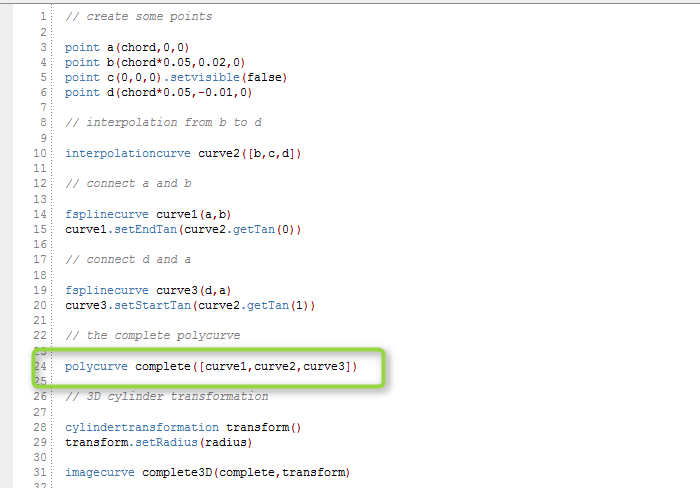
The polycurve receives the 3 input curves (fsplinecurve, interpolationcurve, fsplinecurve) which is highlighted in the final screenshot. The profile is then transformed into the 3D space by using a cylinder transformation. Don’t get scared by the feature programming language – you can set up such a simple example also in the graphical user interface of CAESES®, interactively and without any further programming know-how 🙂
More Information
Do you like this short article? Then please share it with your friends or colleagues. Also check out our product pages for more information about CAESES®.